• The story behind this post
• Introduction
• Traveling Salesman Problem (TSP)
• Initial note
• Solution outline
  • Adaptation
  • Natural selection
  • Matching for the reproduction
  • Create children
  • Crossover
  • Mutation
• Evolution in action
• Conclusion
• Alternative algorithms
  • 1. Brute Force algorithm
  • 2. Dynamic Programming (DP)
  • 3. Greedy algorithm
  • 4. Branch and Bound
  • 5. Ant Colony Optimization (ACO)
  • 6. Simulated Annealing (SA)
  • 7. Artificial Neural Network (ANN)
• Ideas for future work
• Credits

The story behind this post

During my Christmas break, I found a blog post from Peter Brookes-Smith Darwin and The Traveling Salesperson. He wrote, that he was looking for some project for his holidays. He found the blog post that inspired him to start the project and solve the problem by himself without finishing the article. It was similar to my case. I had genetic algorithms in the back of my head for a long, long time. Now while having some spare time between Christmas and New Year - I decided to get my feet wet on that topic.

Introduction

Are you familiar with the Traveling Salesman Problem (TSP)? It's a classic problem in computer science where a salesman is tasked with visiting a set of cities once and returning to the starting place, with the goal of finding the shortest possible route. Tackling the TSP problem can be very challenging, particularly as the number of cities increases. In this blog post, we will explore how to use genetic algorithms to solve TSP problem. We'll take an in-depth look at the different steps involved in the algorithm, along with the results obtained. We'll also provide an overview of the other algorithms that are used to solve TSP, and the comparison with genetic algorithm. Our goal is to provide an easy-to-follow guide that will help you understand the basics of using genetic algorithms to solve TSP, and to inspire you to try your hand at this fascinating problem.

Traveling Salesman Problem (TSP)

The problem can be defined like this: having a list of cities and finding the shortest route for a salesman to visit each of them once and come back to the starting place.

For non-trivial cases of a few cities, the computational complexity for brute force search is high. The total number of unique routes (\(TNUR\)) is:

To help to grasp the order of complexity - when the number of cities grows beyond ~25, the time required to brute force search for an optimal solution would exceed the age of the known universe.

The traveling salesman is a beautiful problem to test various optimization algorithms against it. A big portion of metaheuristic solutions came from the evolution algorithm family.

Initial note

This post is the recording of an almost naive attempt to apply the evolution approach to solve the problem. Before writing this post, on purpose, I haven't done solid education on genetic algorithms so the terminology and methods might not correspond to ones established in the field. The positive side of this approach is that fun was not spoiled with existing solutions. This I meant as a fun project, not a conference paper. When the disclaimer was done, let's go to the problem-solving.

Solution outline

The idea for finding the best route using mechanisms that are available in nature in the evolution process described by Karol Darwin is as follows: Algorithm initialization:

1. Draw initial population of solutions - set of random routes (e.g. 500 routes). then, in the loop run epochs of evolution steps;
2. Adaptation - corresponds to minor improvements that an organism is able to implement in order to better fit into the environment;
3. Natural selection - corresponds to challenges, threads posted by nature that strong organisms are able to handle and survive and weak units are lost;
4. Matching for reproduction - match members of the population in pairs to prepare for the reproduction
5. Create children - new organisms are born and their genome (route) consists of parts of routes coming from both parents (crossover mechanism). Add mutation to introduce further variation in the population;
6. Repeat the cycle - go to step 1, and start a new epoch.

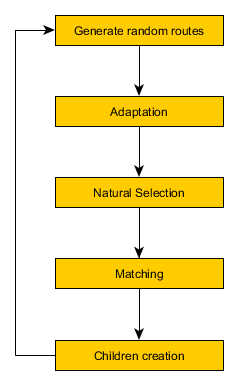
Figure 1. Steps of evolution algorithm

Adaptation

I decided to include mechanisms for minor, local improvements that in nature, organisms might be able to perform to better fit the environment. The implementation of the adaptation is twofold:

1. Swap two consecutive cities on the list that represents the route and check if the change brought an improvement - if so, keep the change and check another pair of cities until the end of the list.
2. Reverse three elements route segments and similarly, as in the previous method - keep the change if the new, candidate route with the reversed segment is shorter than the version with the non-reversed segment. Both are implemented "swapper" or "reverser" as moving along the list of cities in the route.

Natural selection

Natural selection allows to remove of poor solutions and makes room for new experimental variants of routes that inherit features from the best solutions found so far. The implementation was to sort the solutions in the ascending order and keep only 10% of the best solutions.

Matching for the reproduction

"Elite" selected in the natural selection step is then used to create pairs of parents to be used in the single act of reproduction. The pairs were drawn randomly with returning, but the random distribution was not uniform. The shortest route of the solution, the higher chance that the solution will be taken as a parent. The probability of selecting the solution was proportional to the inverse of the solution route length i.e. the shorter route - a higher probability to be drawn as a parent. The given organism could be selected as a paired element for multiple reproductions - which should be the case, especially for best-fitted solutions (ones with the shortest route).

Create children

In the process of reproduction always two children were born: one that was the effect of crossover routes from mother and father and the second, based on the same crossover but with mutation added. When drawing pairs, the organism is assigned to the role of mother or father which is important only for the crossover process.

Crossover

In crossover selected segment of a given length (e.g. 5 cities) of the route from the father is being injected into the mother's route. The starting element of the segment in being found in the mother's route and the mother's route is divided into three parts: before the "anchor" element, "anchor" element, and after the "anchor" element. The "anchor" element is replaced by injection. In the next steps mother's route is cleaned up in order to remove duplicate cities (those that appeared in the injection from the father). The cities from the injection were removed from the before anchor and from the after anchor part.

Mutation

The children obtained by applying crossover are then duplicated to have a second child that will be additionally mutated. The mutation is implemented as the random swap of two cities in the list.

Evolution in action

The whole setup of the experiment is highly parameterised and gives endless opportunities to experiment with various setups. The results shown in this blog were produced for this parametrization:

# number of cities
num_cities = 80

# size of initial population (number of initial random routes)
num_routes = 400

# fraction of organisms that survives natural selection process
survival ratio = 0.1

In the first step of implementation, I was able to measure the effect of local adaptation and the gains achieved with this mechanism. While running a single swap of two elements and single reverse or three elements segment gains on random routes were up to 1%. Graphical representation of the route changes confirms that improvement was small - routes still have a high degree of randomness and are far from optimal.

In the next step, I brought this adaptation process to an extreme number to check its potential - what maximum improvements are possible here. Of course, achieving stabilization of the results here would be difficult but I verified what will happen when we change a number of two- and three elements reversing cycles from 1x to 100x times. The improvements achieved in this configuration were XX on average.

The next step involved the full process and proved crossover and mutation to be efficient for improving solution quality i.e. finding as short route as possible.

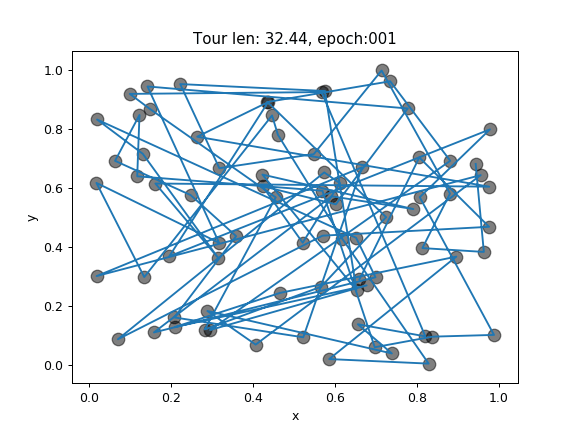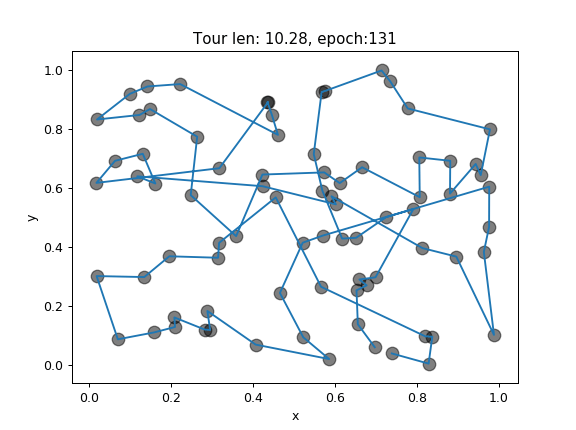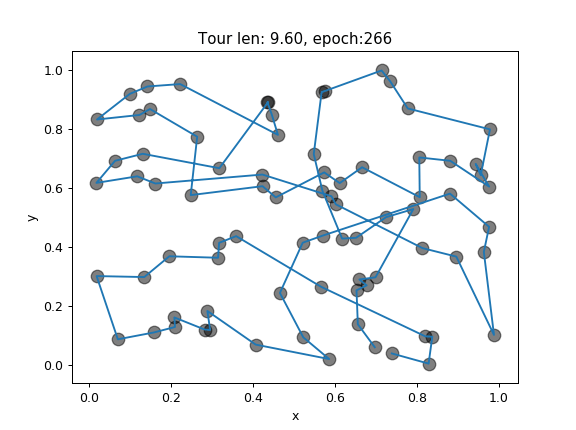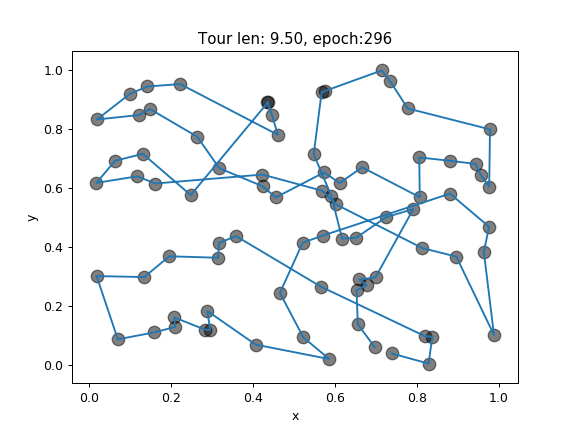
Figure 2. Visualization of best route found in each epoch

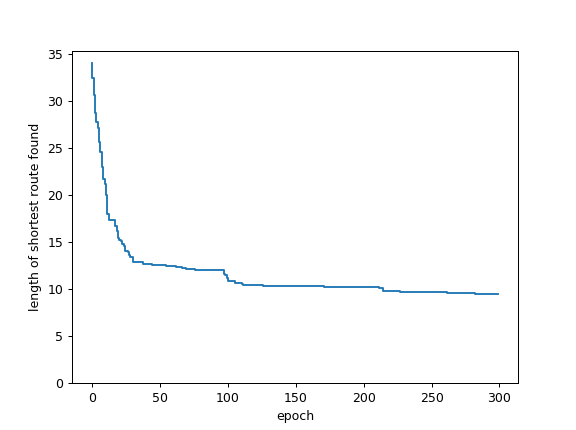
Figure 3. Length of shortest route found in the given epoch of evolution process

Conclusion

1. The experiment showed me the beauty of the evolutionary approach - directed but random evolution leads to the emergence of the order and optimized solutions (however not optimal solutions).
2. The fitness of the solution is stabilizing after ~100 epochs. The population doesn't have sufficient new genomes and variation decreases. With this, the ability to overcome imperfections in the best route found so far drops significantly.
3. Being under the impression of the robustness of the evolutionary system I'm eager to try the evolutional approach as an alternative to Reinforcement learning such as described on openai blog
4. Technical one: even such a side project playing with numerical problems benefits from accompanying tests. Many annoying bugs that appeared during the implementation (mainly from a global range of variables), and covering (at least partially) code with tests helped out to progress.

Alternative algorithms

There are several other algorithms that can be used to solve the Traveling Salesman Problem (TSP):

1. Brute Force algorithm

It is the most simple algorithm for solving TSP problem, where it checks all possible routes one by one and select the one with the minimum distance. However, the time complexity is high, and it is not efficient for a large number of cities.

2. Dynamic Programming (DP)

It is a method of solving problems by breaking them down into smaller overlapping sub-problems and solving each of them independently. DP can be used to solve TSP by building a table of all possible sub-tours, and the optimal solution is constructed using the entries in the table.

3. Greedy algorithm

It is a simple, intuitive and efficient algorithm. Greedy algorithm solves TSP problem by building a solution incrementally, choosing the next city to add to the tour based on the nearest neighbor criterion.

4. Branch and Bound

It is a method that allows us to explore all possible solutions while avoiding the ones that are obviously suboptimal. Branch and Bound uses the concept of lower bound and upper bound to prune the branches that cannot give a better solution than the best solution found so far.

5. Ant Colony Optimization (ACO)

It is a swarm intelligence-based algorithm. The ACO algorithm simulates the behavior of ants searching for the shortest path from their colony to a food source. The ants leave pheromones on the path they travel, and the path with the highest concentration of pheromones is likely to be the shortest path.

6. Simulated Annealing (SA)

It is a probabilistic technique for approximating the global optimum of a given function. SA algorithm starts with a random solution and then repeatedly makes small changes to the solution in the hope of finding a better solution.

7. Artificial Neural Network (ANN)

it is a machine learning algorithm that can be used to model the TSP problem and find an approximate solution. ANN algorithm learns from historical data, and

There is website with multiple algorithms and animated solutions of TSP problem: 11 Animated Algorithms for the Traveling Salesman Problem

Ideas for future work

• Deploy it in the server-less mode of operation. Route calculations and transformations are great candidates for "lambda" functions.
• Use GPU to compute things in parallel
• Overcome stagnation of evolution by evolving several populations independently and allowing for contact between populations from time to time - transfer some solutions from one to another population.

Credits

Cover image from https://commons.wikimedia.org/wiki/File:High_School_Biology_1-13.pdf by CK-12 Foundation on CC license

Any comments or suggestions? Let me know.